Mean median and mode toads – Embark on a ribbiting journey into the world of statistics with mean, median, and mode toads! These statistical measures are the go-to tools for understanding the central tendencies of any toad-related dataset.
From the tiniest tadpole to the grandest toad, these measures will help us uncover the patterns and trends hidden within the vast world of amphibian data.
Introduction
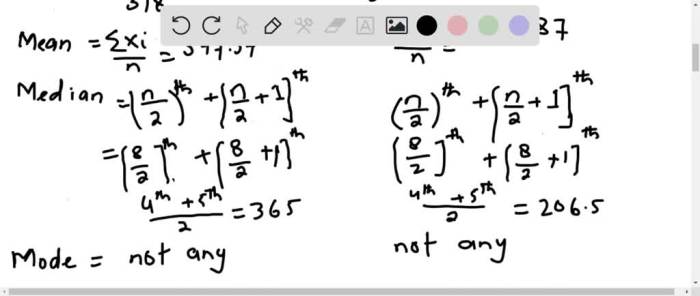
In statistics, measures of central tendency are used to describe the average or typical value of a set of data. Three common measures of central tendency are mean, median, and mode.
Meanis the sum of all values divided by the number of values in a data set. It is also known as the average. Medianis the middle value of a data set when assorted in order from smallest to largest. Modeis the value that occurs most frequently in a data set.
Differences between Mean, Median, and Mode
The mean, median, and mode can all provide different values for the same data set. The mean is sensitive to outliers, which are extreme values that are much larger or smaller than the other values in the data set. The median is not affected by outliers, but it can be misleading if the data set has a large number of ties.
The mode is the most stable of the three measures of central tendency, but it can be misleading if the data set has multiple modes or no mode at all.
Calculating Mean, Median, and Mode
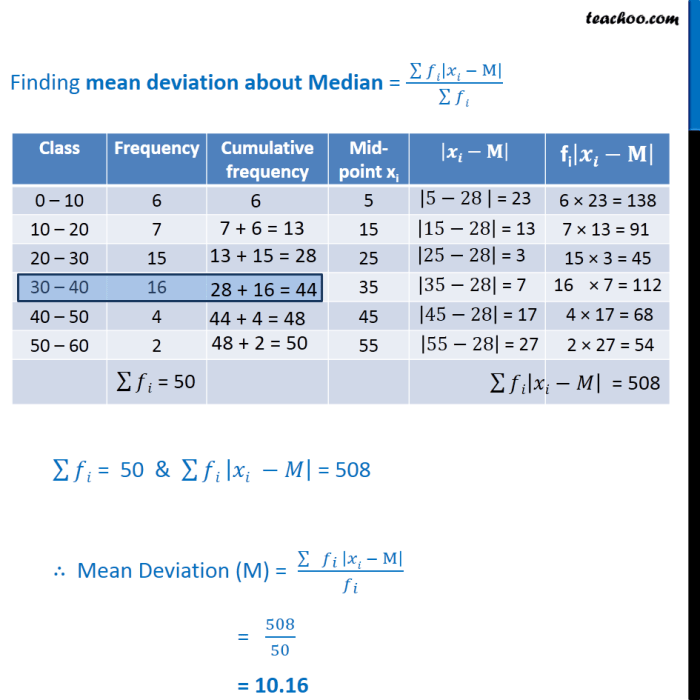
Calculating mean, median, and mode are essential statistical measures used to summarize and analyze data. Each method provides different insights into the central tendency of a dataset.
Calculating the Mean
The mean, also known as the average, is the sum of all values in a dataset divided by the number of values. It represents the central point of the data distribution.
- Add up all the values in the dataset.
- Divide the sum by the number of values.
Calculating the Median
The median is the middle value in a dataset when arranged in ascending or descending order. It represents the value that divides the data into two equal halves.
- Arrange the values in the dataset from smallest to largest.
- If there is an odd number of values, the median is the middle value.
- If there is an even number of values, the median is the average of the two middle values.
Calculating the Mode
The mode is the value that appears most frequently in a dataset. It represents the most common value.
- Identify the value that occurs the most number of times.
- If there is a tie, the dataset is said to be bimodal or multimodal.
Applications of Mean, Median, and Mode
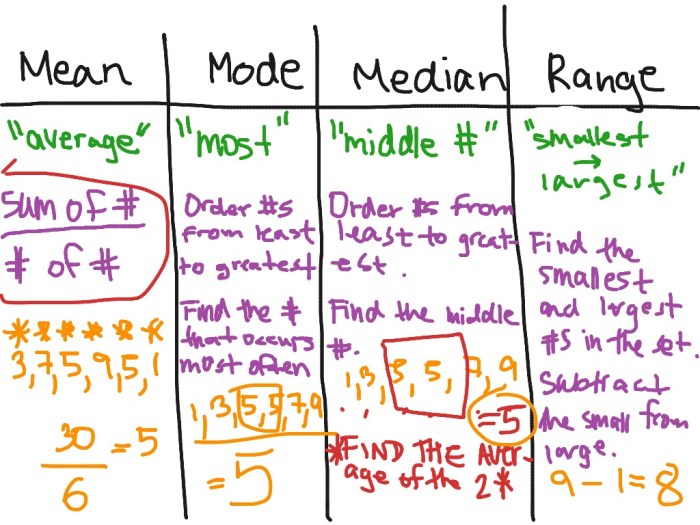
Mean, median, and mode are statistical measures that provide valuable insights into data sets. They are widely used in various fields, including research, business, and everyday life.
The choice of which measure to use depends on the nature of the data and the specific information one wishes to convey. Here are some examples of how each measure is applied in real-world scenarios:
Mean
The mean, also known as the average, is the sum of all values divided by the number of values in a data set. It is commonly used to represent the “typical” value in a distribution.
- Example 1:A company calculates the mean salary of its employees to determine the average compensation within the organization.
- Example 2:A researcher calculates the mean test score of a group of students to assess their overall performance.
Median, Mean median and mode toads
The median is the middle value in a data set when arranged in ascending or descending order. It is less affected by extreme values compared to the mean and is therefore a more robust measure of central tendency in skewed distributions.
- Example 1:A city planner uses the median house price to determine the typical cost of housing in a neighborhood, as it is not influenced by a few very expensive or inexpensive homes.
- Example 2:A doctor calculates the median waiting time for patients in a clinic to assess the efficiency of the healthcare system.
Mode
The mode is the value that occurs most frequently in a data set. It is useful for identifying the most common outcome or preference in a distribution.
- Example 1:A clothing store analyzes the mode of shoe sizes sold to determine which size to stock in greater quantities.
- Example 2:A marketing team identifies the mode of customer feedback to understand the most prevalent concerns or preferences among their clientele.
Advantages and Disadvantages of Mean, Median, and Mode

In statistics, measures of central tendency are used to describe the typical value of a set of data. The three most commonly used measures of central tendency are the mean, median, and mode. Each measure has its own advantages and disadvantages, depending on the data set and the purpose of the analysis.
Mean
The mean, also known as the average, is calculated by adding up all the values in a data set and dividing by the number of values. The mean is a good measure of central tendency when the data is normally distributed, meaning that the values are spread out evenly around the mean.
However, the mean can be misleading if the data is skewed, meaning that there are a few extreme values that are much larger or smaller than the rest of the data. In such cases, the median or mode may be a better measure of central tendency.
Mean, median, and mode are three different ways to measure the central tendency of a data set. If you’re looking for a more in-depth understanding of these concepts, check out Mark K’s lecture notes . They provide a clear and concise explanation of these statistical measures.
Returning to our discussion of mean, median, and mode, it’s important to note that each of these measures has its own advantages and disadvantages.
Median, Mean median and mode toads
The median is the middle value in a data set when the values are arranged in order from smallest to largest. The median is not affected by extreme values, which makes it a good measure of central tendency for skewed data.
However, the median can be difficult to calculate for large data sets, and it can be less informative than the mean when the data is normally distributed.
Mode
The mode is the value that occurs most frequently in a data set. The mode is a good measure of central tendency when the data is clustered around a single value. However, the mode can be misleading if there are multiple modes or if the data is evenly spread out.
Example Dataset: Mean Median And Mode Toads
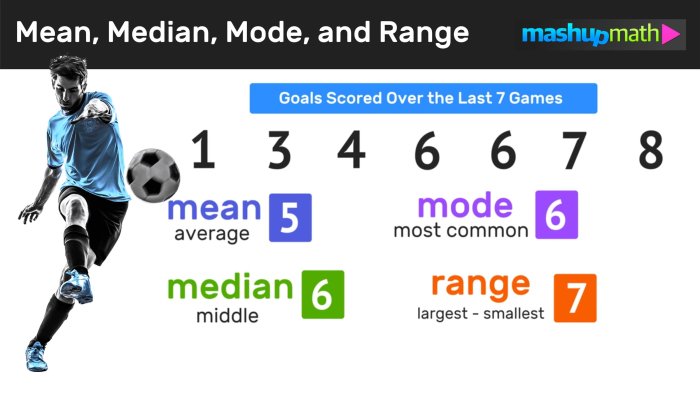
To demonstrate the calculations of mean, median, and mode, we will use a dataset that includes the following information related to toads:
We have organized the dataset in an HTML table with responsive columns for easy viewing:
| Toad ID | Weight (grams) | Length (cm) |
|---|---|---|
| 1 | 25 | 10 |
| 2 | 30 | 12 |
| 3 | 28 | 11 |
| 4 | 25 | 10 |
| 5 | 32 | 13 |
Calculating Mean, Median, and Mode
Using the values in the dataset, we can calculate the mean, median, and mode as follows:
- Mean:The mean is the sum of all values divided by the number of values in a dataset. In this case, the mean weight of the toads is (25 + 30 + 28 + 25 + 32) / 5 = 28 grams.
- Median:The median is the middle value in a dataset when assorted in numerical order. In this case, the weights of the toads can be assorted as 25, 25, 28, 30, 32. The median weight is 28 grams.
- Mode:The mode is the value that occurs most frequently in a dataset. In this case, the weight of 25 grams occurs twice, while all other weights occur only once. Therefore, the mode of the dataset is 25 grams.
Interpreting the Results
The mean, median, and mode provide different insights into the data:
- Mean:The mean gives us the average weight of the toads in the dataset. It is a good measure of central tendency when the data is normally distributed.
- Median:The median gives us the middle value of the dataset. It is not affected by outliers, which are extreme values that can skew the mean.
- Mode:The mode gives us the most common weight of the toads in the dataset. It is a good measure of central tendency when the data is skewed or has multiple peaks.
In this example, the mean, median, and mode are all close to each other, indicating that the data is approximately normally distributed and that there are no significant outliers.
Popular Questions
What’s the difference between mean, median, and mode?
Mean is the average, median is the middle value, and mode is the most frequently occurring value.
How do I calculate the mean of a dataset?
Add up all the values and divide by the number of values.
When should I use the median instead of the mean?
Use the median when there are extreme values in the dataset that could skew the mean.