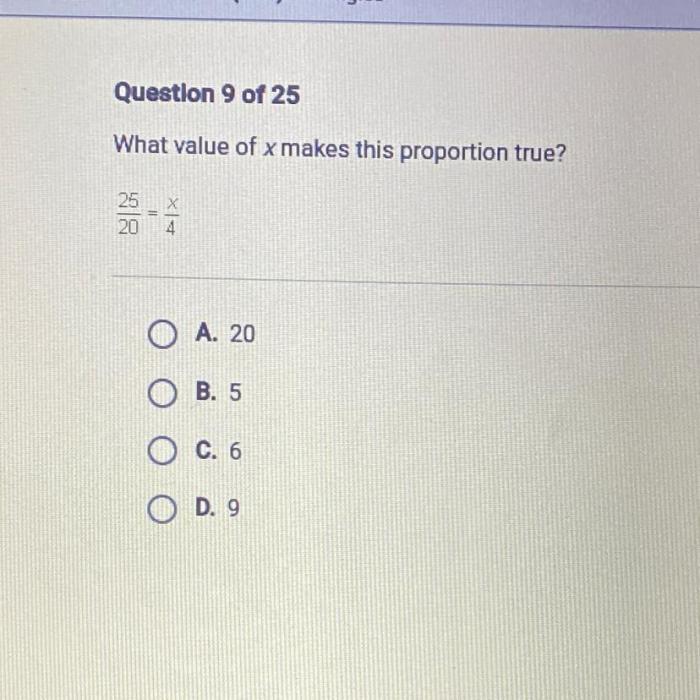
Exploring the concept of proportions in mathematics, this comprehensive guide delves into the enigmatic question: “What is the value of x in the proportion below?” Embark on a journey through the intricacies of proportions, unraveling their applications, complexities, and significance across various disciplines.

Proportions, mathematical equations that equate two ratios, play a pivotal role in problem-solving and understanding relationships between quantities. By examining the steps involved in solving proportions, we gain insights into the techniques and strategies employed to determine the unknown value of x.

This exploration unveils the power of proportions, empowering us to navigate real-world scenarios with precision and confidence.

1. Definitions

In mathematics, a proportion is an equation that states that two ratios are equal. A ratio is a comparison of two quantities, and it is expressed as a fraction. For example, the ratio of 2 to 3 is written as 2/3. A proportion is written as a fraction with an equals sign between the two ratios.

For example, the proportion “2/3 = 4/6” means that the ratio of 2 to 3 is equal to the ratio of 4 to 6.

The value of x in a proportion is the unknown quantity that makes the proportion true. For example, in the proportion “2/3 = 4/x”, the value of x is 6, because 2/3 = 4/6.

2. Solving Proportions

To solve a proportion for the value of x, you can use the following steps:

1. Cross-multiply the numerator of the first ratio with the denominator of the second ratio.
2. Cross-multiply the denominator of the first ratio with the numerator of the second ratio.
3. Set the two products equal to each other.
4. Solve the equation for x.

For example, to solve the proportion “2/3 = 4/x”, we can use the following steps:

1. Cross-multiply the numerator of the first ratio with the denominator of the second ratio: 2
   • x = 3
   • 4.
2. Cross-multiply the denominator of the first ratio with the numerator of the second ratio: 3
   • 2 = 4
   • x.
3. Set the two products equal to each other: 2x = 12.
4. Solve the equation for x: x = 6.

3. Applications of Proportions

Proportions are used in a wide variety of real-world applications, including:

• Scaling recipes
• Mixing paints
• Solving geometry problems
• Calculating distances
• Predicting future events

For example, a baker might use proportions to scale a recipe up or down, depending on how many people they are baking for. A painter might use proportions to mix different colors of paint to create a desired shade. A surveyor might use proportions to calculate the distance to an object that they cannot reach directly.

4. Common Errors

There are a few common mistakes that people make when solving proportions. These mistakes include:

• Not cross-multiplying correctly.
• Dividing by zero.
• Assuming that the value of x is always positive.

To avoid these mistakes, it is important to be careful when solving proportions and to check your work carefully.

Top FAQs: What Is The Value Of X In The Proportion Below

What is the first step in solving a proportion?

Cross-multiply the numerators and denominators of the two fractions.

What are some common applications of proportions?

Scaling recipes, calculating discounts, and converting units of measurement.

How can I avoid common errors when solving proportions?

Ensure that the cross-products are equal and check your solution by substituting the value of x back into the original proportion.